Our favorite Bookworm has one of her illustrated editions posted this morning. I snagged two items as particularly relevant to a phenomenon I’ve known about for some time, but which other people have a hard time digesting. Here they are:
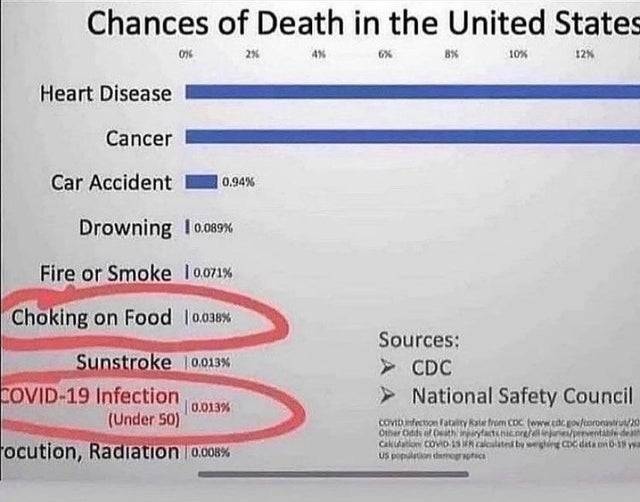

Let’s overlook, just for the moment, that any Gentle Reader of Liberty’s Torch can and will easily grasp the import of the numbers in those two graphics. Rather, let’s reflect on the huge number of people who’ll look at those numbers and utterly fail to understand them. You can trust me on this one, friends: upon confronting those graphics, the great majority of Americans would simply scratch their heads and say “So what?”
The problem isn’t stupidity. Neither is it ignorance. It’s a far simpler thing:
Our lives are lived within a relatively narrow numerical range: countable objects that have perceptible dimensions. We have a feel for those numbers. We lack such a feel for the much larger or the much smaller. It’s what makes the probabilities in the graphics above difficult for most people to appreciate.
Astronomers have that problem too. We don’t use the units that apply to terrestrial distances when speaking of the distances between the planets, or the spaces between the stars. We use units that bring the numbers attached to them into our comfort zones: AUs and parsecs. Those “oversized” units wouldn’t fit anything in normal, terrestrial life, but they’re eminently suitable to astronomical operations.
They who study the very small use special units as well: the Angstrom (Å) and the Electron Volt (eV) are two examples. Indeed, even in the realm of the relatively small, such as genetic studies, we use units normal people doing normal things would not grasp: the micrometer (μm) and microgram (μg) being the most relevant. The point, as previously, is to bring the numbers attached to those units into the realm of the easily grasped and manipulated.
This is something to keep in mind whenever you seek to introduce very large or very small numbers into an argument.
Consider an argument about automobile safety that I encountered long ago: the probability that some individual American will die in an auto accident. Back then, there were about 50,000 road deaths in an average year. That number has considerable emotional impact – My God! 50,000 corpses per year! — but just how threatening is it to the average commuter?
A little arithmetic changes the picture from one that looks like an undertaker’s dream to something the ordinary American driver can – and does – tolerate. Let the total population of the U.S. be set at 250,000,000, just for round number convenience. In a given year, of 50,000 of those Americans will die in a road accident, that’s 50,000 / 250,000,000 == .0005 or 0.05% of the population. In other words, 99.95% of all Americans will escape death by auto that year. (Something else might get you, but that’s for another day.) That should make the average guy feel pretty safe, no?
Well, maybe and maybe not. A lot of people have difficulty with percentages of that sort. Also, there are always custard-heads out there who’ll say something stupid such as “Yes, but the probability of dying from AIDS is 100% if you catch it!” So I did a little more figuring, based on the average number of miles driven per American per year, and it worked out that John Q. Public, to have an even-money chance (probability 0.50) of dying in a road accident, would have to drive 47,000,000 miles: nearly 2000 times around the world at the equator.
The busiest salesman I’ve ever known didn’t quite log 10,000,000 miles over a fifty-year career…and he did almost all of that by air. Stretches the mind, doesn’t it?
I wrote the above partly for your amusement, but also for your perspective. To reach the average person with an important fact, you have to bring any figures important to it into the realm with which he’s comfortable. Numbers with a lot of digits, whether before of after the decimal point, usually don’t qualify. They might seem comprehensible to you, you bulging egghead, you, but the person to whom you’re talking might not share your perspective. Indeed, he probably doesn’t and never will.
Just a few thoughts for your Holy Thursday morning.















4 comments
Skip to comment form
I curse the chuckleheads that decided to ruin grade-school math. Too many kids are incapable of using basic arithmetic without a calculator; even with it, their understanding of how the process work – a “feel for numbers” – is lacking.
So, although a tenacious student can memorize enough to handle the most basic operations, their shaky grasp on the “why am I doing this operation” leaves them with little hope of handling higher level math.
But, never fear!
The education system has decided to “rename” many of the concepts introduced in elementary school. For example, did you know that parents and the students will be told they are learning calculus in primary school?
https://www.theatlantic.com/education/archive/2014/03/5-year-olds-can-learn-calculus/284124/
I do hope those parents realize that such activities don’t work for most kids.
I was lucky. When I was in upper elementary school, New Math was the cutting edge practice. I tried, I really did. But the entire thing made little sense to me.
When I went home, I complained to my mother. She talked to my father, and he sat down with me. I showed him the procedures we were supposed to use for solving problems.
He looked it over, and said, “Well, I suppose you COULD solve it that way, but let me show you an easier way.” Which he did – with great success.
I managed to stumble through the next few years, always getting assistance from my father, as needed. Only when I took a traditionally taught Algebra I class did my confidence return.
When I taught Chemistry, the math was often the hardest for students (WHY schools insist on teaching Chem first, then Physics, is something I will never understand. Oh, I know it was because the Physics taught involved Calculus, but, in fact, many students who take that class have a weaker understanding of basic mechanics than the Conceptual Physics students.).
I handled the math by reaching back to my father’s traditional methods. So, 21st century students were being taught using math that had been common in the 1930s – and, it worked. My students were generally quite successful.
Hmmmm…..
Isn’t interesting, two of the items “highlighted” above, with the lowest chance of impacting us, are both in the top five of “things needing to be controlled by your government(tm)”. The manufacturing of a fake pandemic for one, and the constant effort(s) to erode ones ability to practice the other, makes one wonder.
If only there was a tool, a method universally understood to be impartial in its application. One which, properly applied, would be able to buttress many a reasoned and logical argument/presentation.
Perhaps if Math was once again taught as a “hard science”, based on “fact” and not used as a teaching aid in advancing social agendas, we might arrive at a society who are at least 50% capable of understanding basic mathematical concepts.
But feelings and fear brought about by propaganda and lies, rule the day. And we are the lesser for it.
I started out looking at the thing that popped out at me – the misuse of significant digits. There simply isn’t enough precision in the input data to say “you have a 0.00010256410256% chance of death by firearm.”
There are three significant digits in the population (312 million) and four in the number of deaths (1712), and you never use more than the smallest number of significant digits or three in this case. You have to be careful about zeroes and whether they’re significant or not, and I think it’s fair to ignore the leading zeroes when you count your three digits, so the answer should be 0.000103% chance. Except it’s not. If you divide 1712 by 312 million, that’s .000549%.
And then I tried to get to 1,712 deaths given those numbers they exclude and can’t get there. It’s like someone took a set of numbers that gave the results they quote and then just adjusted one or two numbers so now you can’t do any math to back up the rest of the meme.
This is the fun you have being OCD about numbers…
I’m of the same age as Miss Fox and Mr. Porretto. I worked in construction. Specifically I determined roof and floor support structures used in the construction of homes. I also designed new homes for several years toward the end of my working career. I’ve never been great at math. But, I used it every day for nearly 40 years of my professional life. Late in my career if occurred to me that I used the “older” mathematical methods, but that I also used some of “new math” and some of the current “core” math methods.
What I found was that the method of achieving the result could vary to answer a question. More importantly I had to learn to envision the solution and the logical steps to achieve that solution. Mistakes could cause bodily harm. I’m not an engineer and I had a computer program to produce the expected result, but I had to see that result before I could input the information.
Todays roof and floor truss designers have computer programs that do all of that thinking.
Think of it this way: Humans have not only survived, they’ve thrived. No matter what has happened, war, pestilence, disease. People no longer see through a problem. They no longer learn to envision a solution. Will they survive their lack of vision?